algospot.com/judge/problem/read/FENCE
algospot.com :: FENCE
울타리 잘라내기 문제 정보 문제 너비가 같은 N개의 나무 판자를 붙여 세운 울타리가 있습니다. 시간이 지남에 따라 판자들이 부러지거나 망가져 높이가 다 달라진 관계로 울타리를 통째로 교체
algospot.com
<문제>
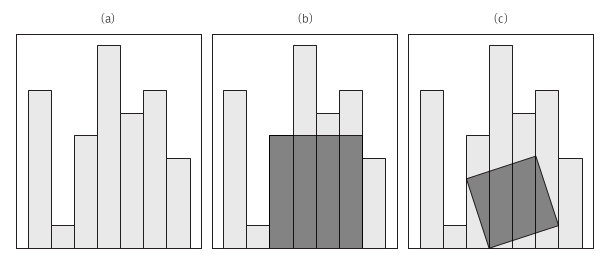
너비가 같은 N개의 나무 판자를 붙여 세운 울타리가 있습니다. 시간이 지남에 따라 판자들이 부러지거나 망가져 높이가 다 달라진 관계로 울타리를 통째로 교체하기로 했습니다. 이 때 버리는 울타리의 일부를 직사각형으로 잘라내 재활용하고 싶습니다. 그림 (b)는 (a)의 울타리에서 잘라낼 수 있는 많은 직사각형 중 가장 넓은 직사각형을 보여줍니다. 울타리를 구성하는 각 판자의 높이가 주어질 때, 잘라낼 수 있는 직사각형의 최대 크기를 계산하는 프로그램을 작성하세요. 단 (c)처럼 직사각형을 비스듬히 잘라낼 수는 없습니다.
판자의 너비는 모두 1이라고 가정합니다.
<입력>
첫 줄에 테스트 케이스의 개수 C (C≤50)가 주어집니다. 각 테스트 케이스의 첫 줄에는 판자의 수 N (1≤N≤20000)이 주어집니다. 그 다음 줄에는 N개의 정수로 왼쪽부터 각 판자의 높이가 순서대로 주어집니다. 높이는 모두 10,000 이하의 음이 아닌 정수입니다.
<출력>
각 테스트 케이스당 정수 하나를 한 줄에 출력합니다. 이 정수는 주어진 울타리에서 잘라낼 수 있는 최대 직사각형의 크기를 나타내야 합니다.
예제 입력
3
7
7 1 5 9 6 7 3
7
1 4 4 4 4 1 1
4
1 8 2 2
예제 출력
20
16
8
<아이디어>
분할정복으로 문제를 해결해 나가는데, 전체를 반씩 쪼개나가면서 2개씩 남긴다.
2개중 작은 것을 기준으로 양옆으로 mid까지 합쳐나간다.
그렇게 한 덩어리를 만들고 재귀를 return 하면서 계속 합쳐나가여 최대 직사각형을 구하면 된다.
(쓰다보니까 나도 내가 무슨말을 하는 지 잘 모르겠다..;)
6549번: 히스토그램에서 가장 큰 직사각형
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤
www.acmicpc.net
위 문제와 같은 문제이다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
#include <bits/stdc++.h>
using namespace std;
#define swap(a,b) (a)^=(b)^=(a)^=(b)
#define endl '\n'
typedef long long lld;
int solve(int left, int right, vector<int>& v)
{
if(left==right) return v[left];
int mid = (left+right)/2;
int ret = max(solve(left, mid, v), solve(mid+1, right, v));
int lo = mid, hi = mid+1;
int height = min(v[lo], v[hi]);
ret = max(ret, height*2);
while(left<lo || hi<right)
{
if(hi < right && (lo==left || v[lo-1]<v[hi+1]))
{
hi++;
height = min(height, v[hi]);
}
else
{
lo--;
height = min(height, v[lo]);
}
ret = max(ret, height*(hi-lo+1));
}
return ret;
}
int main()
{
ios_base::sync_with_stdio(NULL);
cin.tie(NULL);
cout.tie(NULL);
int tc;
cin>>tc;
while(tc--)
{
int n;
cin>>n;
vector<int> v(n, 0);
for(int i=0;i<n;i++)
cin>>v[i];
cout<<solve(0, n-1, v)<<endl;
}
return 0;
}
|
cs |
'Problem Solving > 알고리즘 문제해결전략' 카테고리의 다른 글
| [ALGOSPOT] SNAIL (0) | 2021.01.11 |
|---|---|
| [ALGOSPOT] WILDCARD (0) | 2021.01.11 |
| 카라추바 곱셈 알고리즘 (0) | 2021.01.05 |
| [ALGOSPOT] TRIPATHCNT (0) | 2020.11.06 |
| [ALGOSPOT] 타일링 (TILING2) (0) | 2020.11.06 |