출처: algospot.com/judge/problem/read/ASYMTILING
algospot.com :: ASYMTILING
비대칭 타일링 문제 정보 문제 그림과 같이 2 * n 크기의 직사각형을 2 * 1 크기의 타일로 채우려고 합니다. 타일들은 서로 겹쳐서는 안 되고, 90도로 회전해서 쓸 수 있습니다. 단 이 타일링 방법은
algospot.com
타일링 (TILING) 문제에서 좌우 대칭인 경우의 수를 뺀 비대칭 타일링의 갯수를 구하는 문제이다.
DP 문제들 중에서 제일 힘들었던 문제인 것 같다...ㅜ
위 문제를 해결하는 방법은 다음과 같다.
1. 대칭인 부분도 포함하여 구한 다음, 대칭인 부분을 빼는 방법.
2. 대칭인 부분을 처음부터 제외하고 구하는 방법.
두 방법 모두 상당한 사고력을 요하는 것 같다.
아니 그냥 DP 자체가 상당한 사고력 또는 관찰력을 요구한다.
1. 가능한 모든 경우를 구한 다음, 대칭인 부분을 빼는 방법.
일단 가능한 모든 경우의 수를 구한다. -> 피보나치 수열과 같다.
이제 중요한 부분은 대칭인 경우의 수를 빼는 것인데,
전체 길이(N)가 홀수일 때와 짝수일 때를 나누어서 생각해볼 수 있다.
(1). 홀수일 경우
대칭을 이루기 위해서는 정 가운데에 세로로 타일을 놓고 양옆으로 대칭이어야 한다.
전체 길이가 N일때, 정 가운데 타일 하나 빼면 양 옆의 길이가 (N-1)/2 가 된다.
-> 전체 길이가 (N-1)/2 인 경우의 수 만큼의 대칭인 경우의 수가 존재한다.
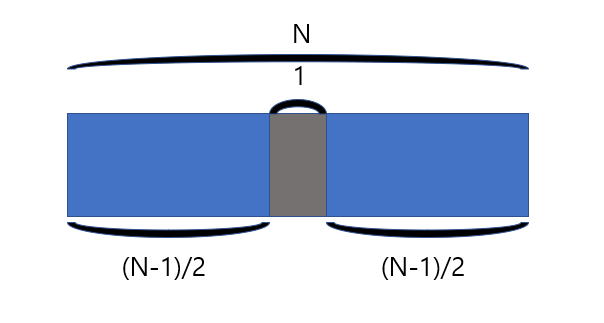
(2). 짝수일 경우
이 때 두가지 경우로 나눌 수 있다.
(2)-1. 정가운데를 나눌 수 있는 경우 -> 정확히 반으로 나눈 양 옆이 같은 모양이다.
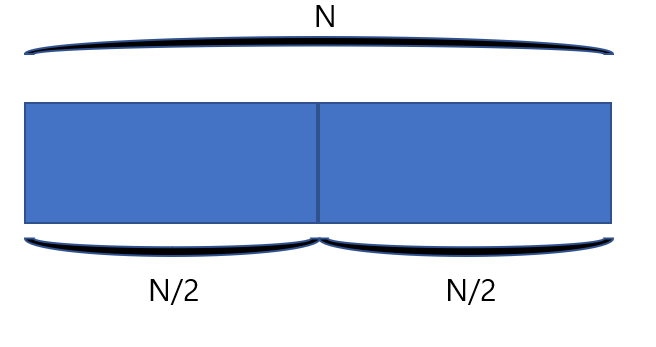
전체 길이가 N/2 인 경우의 수 만큼 대칭이 존재한다.
(2)-2. 정가운데를 나눌 수 없는 경우 -> 가운데에 가로로 이루어진 타일 두개가 있다.
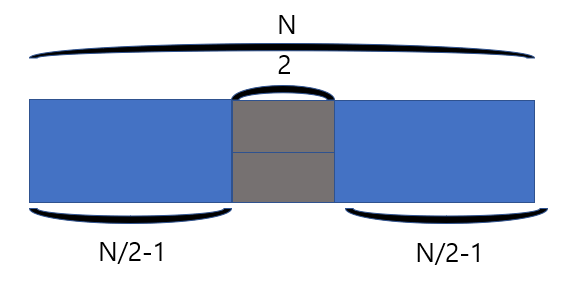
전체 길이가 N/2-1 인 경우의 수 만큼 대칭이 존재한다.
따라서, (N/2 인 경우의 수) + (N/2-1 인 경우의 수) 만큼 빼주면 비대칭 타일링 경우의 수를 구할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include <bits/stdc++.h>
using namespace std;
#define swap(a,b) (a)^=(b)^=(a)^=(b)
#define endl '\n'
typedef long long lld;
#define MOD 1000000007
lld top_down(vector<lld>& v, int pos)
{
if(pos<=1) return 1;
lld& ret = v[pos];
if(v[pos] != -1) return v[pos];
ret = (top_down(v, pos-1) + top_down(v, pos-2))%MOD;
return ret;
}
lld asymmetric(vector<lld>& v, int pos)
{
if(pos%2) return (top_down(v, pos) - top_down(v, pos/2) + MOD) % MOD;
lld ret = top_down(v, pos);
ret = (ret - top_down(v, pos/2) + MOD) % MOD;
ret = (ret - top_down(v, pos/2-1) + MOD) % MOD;
return ret;
}
int main()
{
ios_base::sync_with_stdio(NULL);
cin.tie(NULL);
cout.tie(NULL);
int tc;
cin>>tc;
while(tc--)
{
int n;
cin>>n;
vector<lld> v(n+1, -1);
cout<<asymmetric(v, n)<<endl;
}
return 0;
}
|
cs |
'Problem Solving > 알고리즘 문제해결전략' 카테고리의 다른 글
| [ALGOSPOT] 두니발 박사의 탈옥 (NUMB3RS) (0) | 2021.01.22 |
|---|---|
| [ALGOSPOT] 폴리오미노 (POLY) (0) | 2021.01.22 |
| [ALGOSPOT] SNAIL (0) | 2021.01.11 |
| [ALGOSPOT] WILDCARD (0) | 2021.01.11 |
| [ALGOSPOT] FENCE (0) | 2021.01.05 |

