출처 : algospot.com/judge/problem/read/POLY
algospot.com :: POLY
폴리오미노 문제 정보 문제 정사각형들의 변들을 서로 완전하게 붙여 만든 도형들을 폴리오미노(Polyomino)라고 부릅니다. n개의 정사각형으로 구성된 폴리오미노들을 만들려고하는데, 이 중 세로
algospot.com
<문제>
정사각형들의 변들을 서로 완전하게 붙여 만든 도형들을 폴리오미노(Polyomino)라고 부릅니다. n개의 정사각형으로 구성된 폴리오미노들을 만들려고하는데, 이 중 세로로 단조(monotone)인 폴리오미노의 수가 몇 개나 되는지 세고 싶습니다. 세로로 단조라는 말은 어떤 가로줄도 폴리오미노를 두 번 이상 교차하지 않는다는 뜻입니다.
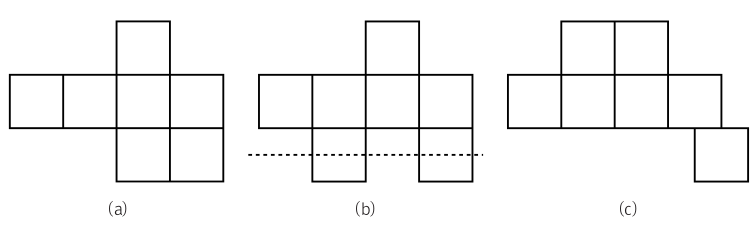
예를 들어 그림 (a)는 정상적인 세로 단조 폴리오미노입니다. 그러나 (b)는 점선이 폴리오미노를 두 번 교차하기 때문에 세로 단조 폴리오미노가 아닙니다. (c)는 맨 오른쪽 아래 있는 정사각형이 다른 정사각형과 변을 완전히 맞대고 있지 않기 때문에 폴리오미노가 아닙니다.
n개의 정사각형으로 구성된 세로 단조 폴리오미노의 개수를 세는 프로그램을 작성하세요.
<입력>
입력의 첫 줄에는 테스트 케이스의 수 C (1≤C≤50)가 주어집니다. 그 후 각 줄에 폴리오미노를 구성할 정사각형의 수 n (1≤n≤100)이 주어집니다.
<출력>
각 테스트 케이스마다, n개의 정사각형으로 구성된 세로 단조 폴리오미노의 수를 출력합니다. 폴리오미노의 수가 10,000,000 이상일 경우 10,000,000으로 나눈 나머지를 출력합니다.
<예제 입력>
3
2
4
92
<예제 출력>
2
19
4841817
풀이방법을 생각해내기 상당히 까다롭고 설명하는 것도 힘든 문제..
이 문제의 핵심은 세로 단조를 어떻게 쉽게 생각하는가 인것 같다.
세로 단조 폴리오미노 이므로 가로줄 관점에서 보았을 때, 블럭들이 서로 붙어있어야하며 떨어져 있으면 안된다.
그럼 우리는 세로 단조의 경우의 수를 세기 위해서 이렇게 생각해볼 수 있다.
N개의 정사각형이 있을 때, 최대 N행을 만들 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
#include <bits/stdc++.h>
#define swap(a,b) (a)^=(b)^=(a)^=(b)
#define endl '\n'
using namespace std;
typedef long long lld;
#define MOD 10000000
int n;
int top_down(int num, int pos, vector<vector<int>>& v)
{
int& ret = v[num][pos];
if(num == pos) return 1;
if(ret != -1) return ret;
ret = 0;
for(int i=1;i<=num-pos;i++)
{
ret += ((pos+i-1) * top_down(num-pos, i, v)) % MOD;
ret %= MOD;
}
return ret;
}
int main()
{
ios_base::sync_with_stdio(NULL);
cin.tie(NULL);
cout.tie(NULL);
int tc;
cin>>tc;
while(tc--)
{
cin>>n;
vector<vector<int>> v(n+1, vector<int>(n+1, -1));
int res = 0;
for(int i=1;i<=n;i++)
{
res += top_down(n, i, v);
res %= MOD;
}
cout<<res<<endl;
}
return 0;
}
|
cs |
'Problem Solving > 알고리즘 문제해결전략' 카테고리의 다른 글
| [ALGOSPOT] 조세푸스 문제 (JOSEPHUS) (0) | 2021.01.22 |
|---|---|
| [ALGOSPOT] 두니발 박사의 탈옥 (NUMB3RS) (0) | 2021.01.22 |
| [ALGOSPOT] 비대칭 타일링 (ASYMTILING) (0) | 2021.01.22 |
| [ALGOSPOT] SNAIL (0) | 2021.01.11 |
| [ALGOSPOT] WILDCARD (0) | 2021.01.11 |

