한 시작점에서 다른 모든 정점까지의 최단 거리(간선 가중치의 합이 최소)를 구하는 알고리즘 중 가장 유용한 알고리즘으로 다익스트라 알고리즘이 있다.
하지만 다익스트라 알고리즘은 음수 간선이 있는 그래프의 경우, 그 정당성이 보장되지 않아 벨만-포드 알고리즘을 사용해야한다.
벨만-포드 알고리즘은 음수 간선이 있는 최단 경로를 찾을 뿐만 아니라, 그래프에 음수 사이클이 있어서 최단 거리가 제대로 정의되지 않을 경우 알려주기도 한다.
벨만-포드 알고리즘
시작점에서 각 정점까지 가는 최단 거리의 상한을 적당히(?) 예측한 뒤, 예측 값과 실제 최단 거리 사이의 오차를 반복적으로 줄여가는 방식으로 동작한다.
수행 과정에서 각 정점까지 최단 거리의 상한을 담은 배열 upper[]을 유지한다.
이 값은 알고리즘이 진행됨에 따라 점점 줄어들고, 알고리즘이 종료할 때는 실제 최단 거리를 담게 된다.
벨만-포드의 동작 과정
시작점을 s 라 하자.
상한을 담은 배열 upper[]를 가지고 있고, 현재 알고있는 정보인 시작점에서 부터 시작점까지 최단거리인 0으로 초기화 한다. -> upper[s] = 0
나머지 원소들은 모두 무한대의 값(아주 큰 수)으로 초기화 하도록 한다.
벨만-포드 알고리즘은 이 예측 값을 실제 최단 거리에 더 가깝게 갱신하기 위해 최단 거리의 특성을 이용한다.
$$ 최단거리의 특성 $$
$$ dist[v] \leq dist[u]+w(u, v) $$
이 조건은 항상 성립한다.
위 조건을 보면 아래 그림이 모순임을 알 수 있다.
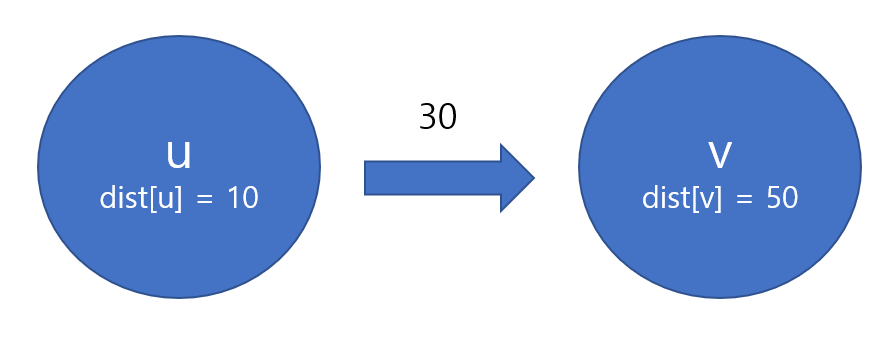
\( (u, v) \) 의 가중치가 30이고, \( dist[u] = 10, dist[v] = 50 \) 이라고 하자.
\( dist[u] = 10 \) 이라는 말은 \( s \) 에서 \( u \) 로 가는 길이 10 짜리 경로가 있다는 말이다.
이 경로 뒤에 \( (u, v) \) 를 붙이면 \( s -> u -> v \) 인 40인 경로를 얻을 수 있다.
그러므로 \( v \) 까지 최단거리 \( dist[v] \) 는 40보다 클 수 없다.
이 속성을 이용하면 upper[]의 값을 조금 더 실제 최단 거리에 가깝게 보정할 수 있다.
\( upper[u]+w(u, v) < upper[v] \) 인 상황을 생각해보자.
\( u \) 까지 가는 최단거리는 항상 \( upper[u] \) 이거나 그보다 짧다.
그 뒤에 \( (u, v) \) 를 붙인 경로의 길이는 최대 \( upper[u]+w(u, v) \) 임을 알 수 있고, \( upper[v] \) 를 \( upper[u]+w(u, v) \) 로 줄일 수 있다.
이와 같은 과정을 통해 \( upper[v] \) 를 감소하는 작업을 \( (u, v) \) 를 따라 완화한하고 말한다.
벨만-포드 알고리즘은 이와 같은 완화 과정을 모든 간선에 대해 반복적으로 실행한다.
완화가 성공할 때마다 upper는 줄어들고, 실제 우리가 원하는 최단 거리에 가까워진다.
'Problem Solving > 알고리즘 문제해결전략' 카테고리의 다른 글
| 무향 그래프에서 단절점 찾기 / 단절선 찾기 (0) | 2022.06.29 |
|---|---|
| 오일러 서킷을 찾아내는 알고리즘 (0) | 2021.03.04 |
| [ALGOSPOT] 단어 제한 끝말잇기 (WORDCHAIN) (0) | 2021.02.18 |
| 오일러 서킷 (Eulerian circuit) (0) | 2021.02.16 |
| [ALGOSPOT] 고대어 사전 (DICTIONARY) (0) | 2021.02.09 |

